
Abbildung 1
Hinweis: für einen einwandfreien Programmlauf wird Java ab Version 1.5 benötigt
|
||
| Die Seiten zu den einzelnen Mustern werden in neuen Fenstern geöffnet. Mittles der Tastenkombination ALT + TAB kann man bequem zwischen Applet, Musterseite und Parameterfenster wechseln. |
In der obigen Liste ein Modell auswählen und dann im Parameterfenster die Parameter mit Hilfe der Schieberegler einstellen. (Nach Betätigen des Schalters "Allgemeine Parameter" kann die Größe des Zellenfeldes - also des Musters - durch Einstellen des rechten und des oberen Zellenrandes eingestellt werden.) Schließlich rechts den Button neue Daten berechnen betätigen. Die Lösung des zugrundeliegenden Differentialgleichungssystems wird nun ermittelt. Das Laufen der Berechnung wird links des Buttons angezeigt; ist sie beendet, erhält man dort die Mitteilung, dass Daten zur Ausgabe zur Verfügung stehen. (Manche Parameterkomibnationen können zu längeren Rechenzeiten führen.) Nun kann die Lösung auf verschiedene Weisen visualisiert werden:
Alle Visualisierungen öffnen neue Fenster, die bei weiteren Aufrufen nicht automatisch wieder geschlossen werden. Um eine Fensterflut zu verhindern, müssen die Fenster einzeln wieder geschlossen werden.
Die Visulaisierungen werden hier nun genauer erläutert:
Die Modelle beschreiben Wechselwirkungen zwischen verschiedenen Substanzen, von welchen genau eine - nämlich immer die erste aufgeführte - für eine Pigmentbildung, also Farbgebung, verantwortlich ist. Die berechnete Lösung des mathematischen Modells gibt für die Punkte des Zellenfeldes an, welche Menge von jeder der beteiligten Substanzen vorhanden ist. Wer mehr erfahren möchte, kann sich hier über die Grundlagen des Modells informieren.
Bei der Anzeige des Musters wird der Wert der für die Pigmentbildung verantwortlichen Substanz
entsprechend seiner Größe in verschiedene Farbwerte umgesetzt.
Wird einer der drei Schalter zur Anzeige des Musters gedrückt, öffnet sich ein neues Fenster,
das das so entstehende Muster sowie Informationen zu den verarbeiteten Werten zeigt.
Bei der Schwellenwert-Version ist zusätzlich ein Schieberegler zu sehen,
über welchen der Schwellenwert verändert werden kann.
Die für die Darstellung des Musters verwendete Farbe kann im Parameterfenster
unter Allgemeine Parameter eingestellt werden.
Sie ist im so genannten
Die Unterschiede zwischen den drei Musteranzeigen:
Muster (absolut)
Der (Lösungs-)Wert 0 entspricht der Hintergrundfarbe Weiß,
der höchste auftretende Wert der vollen Musterfarbe.
Alle Zwischenstufen werden in jeder der drei Farbkomponenten
linear zwischen diesen beiden Farben approximiert.
Muster (relativ)
Wie zuvor, doch wird hier der kleinste auftretende Wert der weißen Farbe zugeordnet.
Muster (Schwellenwert)
Alle Werte oberhalb eines gegebenen Schwellenwertes werden in der vollen Musterfarbe angezeigt,
alle darunter in Weiß. Der Schwellenwert kann über einen Schieberegler im Musterfenster verändert werden.
Im Parameterfenster können unter Allgemeine Parameter
zwei weitere Werte eingestellt werden, die direkte Auswirkungen
(d.h. ohne eine neue Berechnung durchführen zu müssen) auf die Musterdarstellung haben:
Bei der Umsetzung in das Muster werden nicht alle Werte der Lösung verwendet.
Unter Muster nach jeweils ... Rechenschritten weiterzeichnen
kann das Bild in vertikaler Richtung "gezoomt" werden.
Zulässig sind nur positive ganzzahlige Werte (kleine Zahlen = hohe Auflösung).
In vertikaler Richtung werden alle Werte bei der Umsetzung in das Muster verwendet.
Unter das Muster um den Faktor ... in Horizontalrichtung dehnen
kann das Bild horizontal gestreckt werden.
Auch diesmal sind nur positive ganzzahlige Werte zugelassen,
hohe Zahlenwerte führen allerdings nur zu einer vergrößerten Anzeige, nicht zu einer höheren Auflösung.
Die Schneckenschalen entstehen und wachsen durch Anlagerung von weiterem Material entlang einer einzigen Kante, der so genannten Wachstumskante. Das Schalenmuster ist demnach eine zeitliche Aufzeichnung der Abfolge von vielen eindimensionalen Mustern. (Die Konservierung der Zeit ist auch der Grund, warum sich die Schalenmuster zur Analyse des Modells so sehr eignen.) Die filmische Visualisierung animiert die Graphen der Stoffmengen der beteiligten Substanzen über die Zeit. Der Film zeigt also die Veränderungen der Stoffmengen an der Wachstumskante und erhellt so sehr anschaulich die antagonistischen Wechselwirkungen zwischen den beteiligten Substanzen.

Abbildung 1
Nach dem Betätigen des Knopfes Film von der Wachstumskante wird ein Fenster mit Leinwand und Bedienelementen (Abbildung 1) angezeigt. Das Erscheinen kann - gerade bei größeren Modellen - einen Moment dauern. Das Betätigen des Start-Knopfes lässt den Film anlaufen, mittels der Stopptaste kann das Abspielen jederzeit unterbrochen werden. Unten im Bereich Anzeige erscheint eine Liste mit den Substanznamen der beteiligten Stoffe (die Farben korrespondieren mit den Farben der Kurven). Ein Klicken in die kleine Box links eines Stoffes schaltet die Anzeige der zugehörigen Kurve an bzw. aus. Direkt unter der Leinwand läuft ein schwarzer Balken als Zeitanzeige mit. Klickt man mit der Maus auf eine Stelle der Zeitleiste, so wird der Film an der zugehörigen Position fortgesetzt. Die restlichen Bedienungsmöglichkeiten erklären sich von selbst.
Diese Visualisierung orientiert sich stark an der mathematischen Formulierung
des zugrundeliegenden Differentialgleichungssystems.
Dabei unterscheidet man die Ortsrichtung (Variable x, horizontal)
und die Zeit (Variable t, vertikal).
Jeder beteiligte Stoff wird einer Koordinatenfunktion (y1, y2, ...) zugeordnet.
Angezeigt werden die Werte jeder Koordinatenfunktion (entspricht also den Substanzmengen)
an den verschiedenen Stellen in horizontaler Richtung zu einem festen Zeitpunkt t.
(Das entspricht einer horizontalen Linie durch das Zellenfeld auf der Höhe zum Wert t.)
Der Wert t kann mittels des Schiebereglers verändert werden.
Wird dann der Knopf zeichnen betätigt,
werden die Lösungskurven zum aktuellen
Die Anzeige im Koordinatensystem kann verändert werden.
Eine Veränderung des horizontalen Ausschnitts ist am einfachsten durch Ziehen der Maus im Diagramm möglich.
Anschließend wird der Bereich angezeigt,
der zwischen dem Drücken und Loslassen der linken Maustaste mit dem Mauszeiger überstrichen wurde (gelbe Linie).
Durch das Betätigen des Schalters volle
Ansonsten drücke man den Knopf Koordinatensystem.
Es erscheint ein Fenster,
in welchem man den angezeigten Ausschnitt in horizontaler Richtung
Im Parameterfenster lassen sich mit Hilfe von Schiebereglern die einzelnen Modellparameter innerhalb eines vorgegebenen Bereiches verstellen. Bei nicht vorhandenen (oder nicht verstellbaren) Parametern ist das entsprechende Feld mit der Aufschrift im Modell nicht existent versehen (siehe Abbildung 2). Die Einstellung der Parameter, die beim Aufruf des Musters zu sehen ist, lässt sich jederzeit durch Drücken des Buttons Grundeinstellung wiederherstellen rekonstruieren.
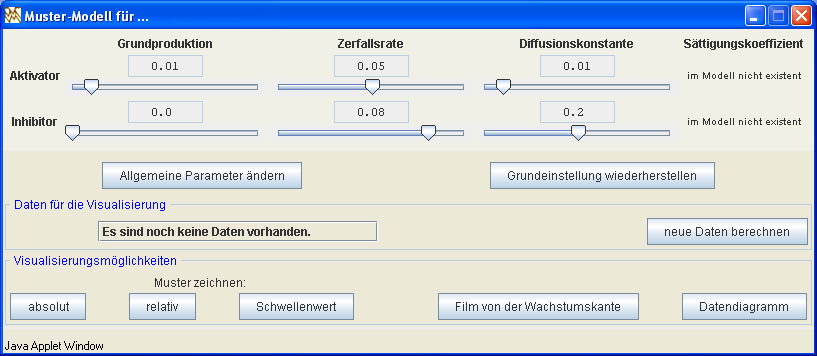
Abbildung 2
Die Bedeutung der Parameter:
Grundproduktion meint zuerst ein von den übrigen Umständen völlig unabhängiges Entstehen des Stoffes.
(Eine von einer oder mehreren Stoffmengen abhängige Produktion nennt man Produktionsrate.)
Die Wirkung auf die Gesamtmenge ist jedoch nicht immer unmittelbar: auch die Grundproduktion kann noch einer
Produktionsrate unterworfen sein. (Die durch die Grundproduktion hinzukommende Menge ist dann das Produkt aus
Grundproduktion und Produktionsrate.)
Eine in allen Modellen auftretende Größe ist die Quelldichte. Das ist eine lokale(!) Produktionsrate,
d.h. sie ist nicht an allen Stellen gleich, sondern unterliegt sehr leichten zufälligen Schwankungen,
wie man es unter natürlichen Bedingungen erwarten darf. Dies ist für die Modelle essentiell, denn die
lokalen Schwankungen stoßen die Mechanismen an, die zur Ausbildung eines Musters führen. Der Grundwert der Quelldichte
ist nicht einstellbar, sondern hat stets dieselbe Größe wie die (zugehörige) Zerfallsrate: das soll helfen,
dass bei den Berechnungen Zahlenwerte der Größenordnung 1 entstehen.
Die Zerfallsrate beschreibt den Anteil an der vorhandenen Stoffmenge, der auf natürliche Art und Weise zerfällt. Sie beeinflusst eine bei den theoretischen Überlegungen wichtige Größe, die so genannte Reichweite eines Stoffes. Damit ist die mittlere Entfernung (Diffusion!) zwischen seiner Produktion und seinem Zerfall gemeint.
Die Diffusionskonstante ist ein Maß für die Ausbreitungsgeschwindigkeit eines Stoffes.
Sättigung bedeutet, dass eine bestimmte Größe nicht ungehemmt anwachsen kann. Sättigungskoeffizienten bestimmen ebenso die Geschwindigkeit, mit welcher die Einschränkungen greifen, wie Maximalwerte, die nicht überschritten werden können. [Mehr dazu findet man beim Modell weitere Streifenmuster.]
Nach dem Drücken des Knopfes Allgemeine Parameter öffnet sich ein neues Fenster (Abbildung 3). Die Zahl der Punkte, an denen Werte der Lösung berechnet werden, lässt sich mittels der Einträge rechter Zellenrand (xr) und oberer Zellenrand (t1) festlegen. (Im Grunde ist die Angabe für die Ausgabe des Musters nichts anderes als die (maximal) angezeigten Pixel (xr x t1)).
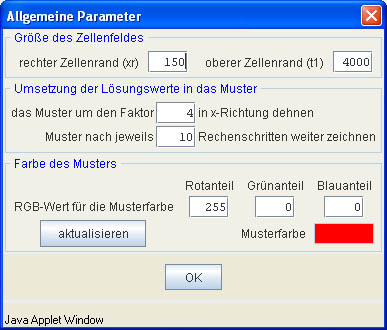 |
| Abbildung 3 |