Rembrandt
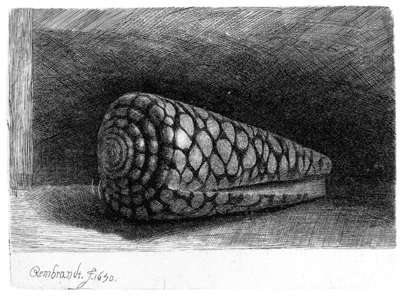
1650 versuchte sich Rembrandt an der Darstellung der Schale der Marmorkegelschnecke (Conus marmoreus). Vergleiche mit Originalen und das Modell zur Simulation des Musters zeigen, dass seine Wiedergabe nicht naturgetreu ausfiel.
Rembrandt

1650 versuchte sich Rembrandt an der Darstellung der Schale der Marmorkegelschnecke (Conus marmoreus). Vergleiche mit Originalen und das Modell zur Simulation des Musters zeigen, dass seine Wiedergabe nicht naturgetreu ausfiel.
 |
 |
 |
 |
| 1 | 2 | 3 | 4 |
 |
 |
 |
 |
| 5 | 6 | 7 | 8 |
Im Modell für die Simulation des Schalenmusters von Conus marmoreus wird das Zusammenwirken zweier Systeme betrachtet.
Beteiligt sind ein
Das System partieller Differentialgleichungen für das Zusammenwirken eines Pigment- und eines Löschsystems lautet wie folgt:
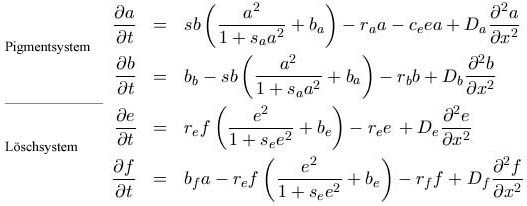
Die beschriebene Wirkung der Systeme aufeinander erkennt man an zwei Termen:
In der Gleichung für den
Um eine reine Zweifarbigkeit des Bildes zu erlangen, empfiehlt sich für die Umsetzung ins Muster die Schwellenwert-Version.
Die Voreinstellungen der Parameter beim Aufruf der Mustersimulation im Applet sind die folgenden:
| Grundproduktion | Zerfallsrate | Diffusionskonstante | Sättigungskoeffizient | |
| Aktivator PS | 0 | 0.01 | 0.005 | 0.05 |
| Substrat PS | 0.1 | 0 | 0 | 0 |
| Aktivator LS | 0.013 | 0.1 | 0.3 | 0.05 |
| Substrat LS | 0.01 | 0 | 0.3 |
Führt man eine Simulation mit diesen Parametern durch, so sieht man ein Muster, das sehr gut dem Ideal des Dreiecksmusters
entspricht und etwa so auf
Wenn das Zustandekommen des Dreiecksmusters aus dem Ringen des Pigment- mit dem Löschsystem verstanden ist,
so lässt sich auch die Wirkung einzelner Parameter leicht erahnen, wenn man ihren Einfluss in den Gleichungen
erkennt. Deshalb sollen jetzt die Beziehungen zwischen dem verbal formulierten Modell, den Gleichungen und dem Muster
ein wenig genauer betrachtet werden.
Wenige in der Anfangssituation pigmentaktive Bereiche
stecken ihre Umgebung an. Die Pigmentaktivierung breitet sich langsam aus,
fördert aber zugleich die Aktivierung des Löschsystems, das sich viel
schneller ausbreitet (große Diffusionskonstanten).
In den Randregionen der sich rasch verbreitenden Löschreaktion können jedoch
(zumindest zunächst) kleine pigmentaktive Bereiche überleben, die sich
vom Zentrum der Löschaktivitäten wegbewegen. Die überlebenden Bereiche
wiederum sind in der Lage, ihre Umgebung anzustecken, was zur erneuten
Ausbreitung der Pigmentaktivierung führt.
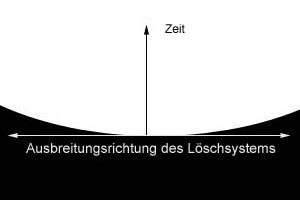 |
| Abbildung 1 |
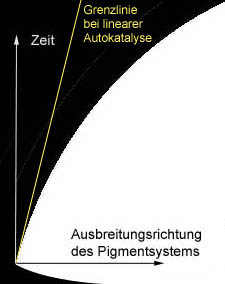 |
| Abbildung 2 |
Kann man die weiter oben gezeigten vielfältigen Variationen allesamt mit diesem Modell nachahmen? Wenn es nicht gelingt,
was sagt das dann über das Modell aus? Alle Parameter lassen sich (hier) nur in einem bestimmten Bereich verändern,
manche Änderungen scheinen kaum Auswirkungen zu haben. Aber Vorsicht: Ein und dieselbe Werteänderung kann völlig anders
wirken, je nachdem welche Werte die übrigen 14(!) Parameter gerade einnehmen.
Hier bleibt jedenfalls viel Platz zum Ausprobieren.
Die folgenden Beschreibungen beziehen sich auf die Veränderung nur des jeweils genannten
Parameters aus der Grundeinstellung heraus:
Die Erhöhung der Grundproduktion führt zu Oszillationen (Streifen parallel zur Wachstumskante).
Wird die Zerfallsrate erhöht, werden die Dreiecke groß und breit.
Ein Absenken der Zerfallsrate führt zu schmalen Dreiecke, die schließlich miteinander verschmelzen.
Eine größere Diffusionskonstante verbreitert die Dreiecke.
Eine kleinere Diffusionskonstante verschmälert entsprechend die Dreiecke; das geht bis hin zum Verschwinden des Musters (Diffusionskonstante 0).
Der Sättigungskoeffizient wirkt auf die Rundung der beiden von der Wachstumskante weg zeigenden Dreieckseiten (s.o.).
Die Erhöhung der Grundproduktion lässt flache, kleine Dreiecke mit größeren schwarzen Bereichen entstehen
(0.4: Ähnlichkeit mit
Die Verringerung der Grundproduktion bläst die Dreiecke auf.
Wird die Zerfallsrate erhöht, werden die Dreiecke spitzer, das Muster regelmäßiger.
Die Grundproduktion beeinflusst die Breite der Dreiecke: hohe Grundproduktion = breite Dreiecke (längeres Wirken des Löschsystems).
Wird die Zerfallsrate verringert, blasen sich die Dreiecke auf
(0.05: Ähnlichkeit zu
Die Erhöhung Zerfallsrate (z.B. 0.15) führt zu Oszillationen: Streifen parallel zur Wachstumskante entstehen.
Änderungen an der Diffusionskonstante verändern Größe und Regelmäßigkeit der Dreiecke leicht.
Die Verringerung der Grundproduktion oder die Erhöhung seiner Zerfallsrate führen
zu breiten weißen Dreiecken
Wird die Zerfallsrate bis zum Maximum (0.2) erhöht, kann sich das Löschsystem nicht behaupten: Die Fläche geht in ein reines Schwarz über.
Die Erhöhung der Grundproduktion (0.016) führt zu vielen kleineren, eng aneinander liegenden Dreiecken
Zur Anzeige des Conus-Musters wurde oben die Schwellenwert-Version empfohlen. Dann lassen sich die schwarzen bzw. weißen Bereiche durch eine Änderung des Schwellenwertes ausdehnen.