Komplexe Muster durch konkurrierende Antagonisten

Muster, die punkten

Aus Sicht der Modellierung sind Streifenmuster simpel, da Oszillationen bzw. zeitliche Konstanz mathematisch recht einfach zu verstehen und schließlich umszusetzen sind. Bei den ebenso simpel anmutenden Punkten sieht die Sache schon anders aus. Man kann allerdings Flecken (Punkte oder kleine Streifen) auch aus Überlagerungen von Streifenmustern gewinnen. Und mit Streifen haben wir ja bereits Erfahrungen gesammelt ...

Modellierung

Dem Aktivator-Substrat-Modell kann man hier bei anderen Simulationen begegnen: Einfach beim Wellenmuster und gar doppelt beim Dreiecksmuster von Conus marmoreus. Auch Aktivator-Inhibitor-Modelle sollten nicht unbekannt sein: Bei den Streifenmustern waren sie zum Einsatz gekommen (hier und hier). Mit beiden Ansätzen lassen sich Streifen senkrecht wie parallel zur Wachstumskante erzielen. Daher ist es schon vom Prinzip her interessant, was passiert, wenn zwei Antagonisten gleichzeitig eingesetzt werden, wobei diese dann so eingestellt sind, dass Tendenzen zum Streifenmuster senkrecht zur Wachstumskante mit Tendenzen zur Oszillation in Konkurrenz treten.
Einem Aktivator-Substrat-Modell wird daher ein zweiter Antagonist in Form eines Inhibitors, wie man ihn vom Aktivator-Inhibitor-Modell her kennt, hinzugefügt. Wir sprechen dann vom Erweiterten Aktivator-Substrat-Modell.

Die mathematische Formulierung

Das System partieller Differentialgleichungen für das Erweiterte Aktivator-Substrat-Modell lautet wie folgt:

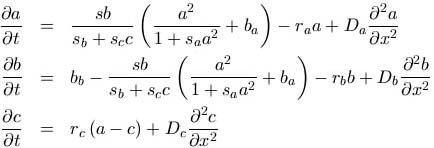
Man erkennt den typischen Zusammenhang zwischen Aktivator und Substrat, wo ein Zuwachs an Aktivator die gleiche Menge an Substrat kostet:

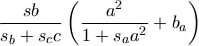
Offensichtlich geht hier ein Sättigungseffekt bezüglich des Substrates ein, wobei die Wirkung des Inhibitors auf den Aktivator in diesen Sättigungsterm mit einbezogen wurde. Die Gleichung für den Inhibitor ist die bekannte, jedoch wird keine Grundproduktion berücksichtigt. Zu beachten ist, dass die Wachstumsrate des Inhibitors dem Wert seiner Zerfallsrate angepasst ist. Wenn im folgenden Abschnitt also von der Zerfallsrate des Inhibitors die Rede ist (so wird der Wert im Parameterfenster zu den Simulationen automatisch benannt), so sollte man im Hinterkopf haben, dass es sich zugleich um die - von der Aktivatormenge abhängige - Wachstumsrate handelt.

Mustersimulation und Analyse

Zum Erweiterten Aktivator-Substrat-Modell gibt es zwei Simulationen. Die Grundeinstellung für die erste der beiden sieht so aus:

	Grundproduktion	Zerfallsrate	Diffusionskonstante	Sättigungskoeffizient
Aktivator	0.01	0.08	0.01	0.1
Substrat	0.08	0	0.3	0
Inhibitor		0.01	0.002	1

Das Muster zu diesen Parametereinstellungen kann sicher nicht einfach genannt werden. Wie kommt es zu Stande? Schaltet man den Inhibitor aus (Wachstums- / Zerfallsrate r_c = 0), so verbleibt ein Aktivator-Substrat-Modell, das Streifen senkrecht zur Wachstumskante produziert. Um die Wirkung des Inhibitors auf den Aktivator zu testen, kann man leider nicht genauso vorgehen und das Substrat ausschalten (siehe Gleichung für Aktivator a). Stärkt man aber die Wirkung des Inhibitors c durch die Einstellungen

	Zerfallsrate	Diffusionskonstante	Sättigungskoeffizient
Inhibitor	0.05	0.01	2

so oszilliert das Muster: Die komplexen Muster, die das Erweiterte Aktivator-Substrat-Modell produziert, entstehen aus einem Ringen der Tendenzen zu parallelen und senkrechten Streifen.
Zurück zur Grundeinstellung: Hier ist die Inhibitorkonzentration so klein, dass eine hohe Substratkonzentration zu ständiger Aktivatorproduktion führt. Senkt man die Grundproduktion für das Substrat ab, setzt die ständige Aktivatorproduktion aus. Es entstehen Wanderwellen. Bei einer noch niedrigeren Grundproduktion lösen sich die Linien mehr und mehr auf. Ein Fleckenmuster entsteht (Grundproduktion b_b = 0.02).

Schauen wir uns nun die zweite Simulation zum Erweiterten Aktivator-Substrat-Modell an. Die Zweitversion zum Modell war für die hier gewählten Einstellungen nötig, weil sie sich teils sehr von den Werten zu den bereits gesehenen Mustern unterscheiden.

	Grundproduktion	Zerfallsrate	Diffusionskonstante	Sättigungskoeffizient
Aktivator	0.005	0.05	0.01	1
Substrat	0.03	0	0	1
Inhibitor		0.02	0.3	2

Wieder bekommt man ein komplexes Muster zu sehen. Schaut man sich das Muster jedoch in der Schwellenwert-Version mit einem Schwellenwert von 0.3 oder 0.4 an, sehen wir ein Fleckenmuster. [Natürlicher erscheint es mit den Umstellungen x_r = 200, t₁ = 5000, Dehnung um Faktor 1 in x-Richtung, weiterzeichnen nach jeweils 20 Rechenschritten, Musterfarbe Schwarz (RGB-Wert 0,0,0) und schließlich Schwellenwert 0.2.]
Schaltet man wie bei der ersten Simulation in der Grundeinstellung durch Nullsetzen der Zerfalls- bzw. Wachstumsrate (r_c = 0) den Inhibitor aus, erkennt man Oszillationen. Auch hier entstehen die komplexeren Muster aus einem Ringen der Tendenzen zu Oszillation (Streifen parallel zur Wachstumskante) einerseits und zeitlicher Konstanz (Streifen senkrecht zur Wachstumskante) andererseits. Es lässt sich also vermuten, dass entsprechend eine Stärkung der Wirkung des Inhibitors gegenüber dem Substrat - äquivalent zu den Untersuchungen bei der ersten Simulation - zu einem senkrechten Streifenmuster tendiert. Mit den einstellbaren Parameterwerten ist dies leider nicht so klar machbar. Stellt man die Wachstums- / Zerfallsrate für den Inhibitor auf 0.08, den Schwellenwert auf 0.6 ein und beobachtet mittels der zugehörigen Visualisierung, was bei einem Absenken seiner Diffusionskonstante (langsamere Verbreitung = lokal stärkere Wirkung) passiert, kann man den Effekt des Inhibitors jedoch recht gut beobachten. Für Diffusionskonstante 0.06 schließlich sieht man sogar das Umschwenken auf das senkrechte Streifenmuster.

zur Einstiegsseite