Wellenlinie bei einer Aktivator-Substrat-Reaktion

Aufschlussreiche Namen

Ein häufig vorkommendes Muster sind Wellenlinien. Oftmals spiegelt sich die Schalenzeichnung im Namen wider. Bei Voluta undulata beschreibt er sowohl das spriralförmige Gehäuse wie das sich darauf befindliche Wellenmuster.

Der Simulation des Wellenmusters beim Applet liegt eine Aktivator-Substrat-Reaktion zugrunde. Der Aktivator a ist verantwortlich für die Pigmentbildung. Zur Entfaltung seiner Wirkung benötigt a das Substrat b, womit das den Modellen eigene Rückkopplungsprinzip bereits geklärt ist: Die Aktivatormenge wird positiv von der Existenz des Substrates beeinflusst, wohingegen die Substratmenge durch den Aktivator reduziert wird. Damit wird sofort klar, dass das System nur bei einem ausreichenden Nachschub an Substrat funktionieren kann.

Mathematische Formulierung und Mustersimulation

Das verwendete System partieller Differentialgleichungen zur Formulierung der Aktivator-Substrat-Reaktion lautet wie folgt:

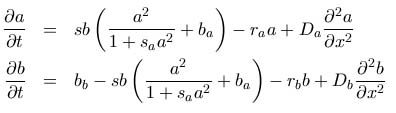
Die Rückkopplungseigenschaften stecken in dem mit unterschiedlichen Vorzeichen versehenen Term .
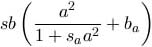Mit diesem Modell lassen sich sehr einfach Oszillationen erzeugen, also Streifen parallel zur Wachstumskante. Bei einer Simulation mit der Grundeinstellung der Parameter sind auch gar keine Wellenlinien zu sehen!

	Grundproduktion	Zerfallsrate	Diffusionskonstante	Sättigungskoeffizient
Aktivator	0.02	0.1	0.003	8
Substrat	0.01	0	0

Eine Veränderung der Substratgrundproduktion beeinflusst bei der Oszillation ihre Frequenz. Das kann man nutzen, um ein Wellenmuster zu produzieren, wenn es gelingt, die Oszillation an verschiedenen Orten verschieden stark werden zu lassen. Dazu ist hier die Substratproduktion ortsabhängig gestaltet. In den oben angegebenen Differentialgleichungen sollte für das Wellenmuster demnach der Ausdruck b_b durch b_b(x) ersetzt werden.

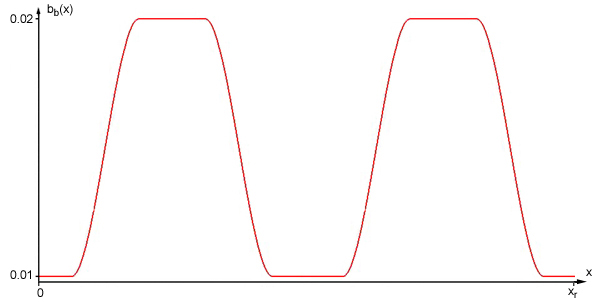Abbildung 1

Die Ortsabhängigkeit der Grundproduktion an Substrat wurde dabei wie folgt realisiert: Der im Parameterfenster angezeigte Wert ist der maximal angenommene. Der Minimalwert ist festgelegt und entspricht mit 0.01 genau der Voreinstellung (rotes Feld der Tabelle) - eine ortsabhängige Variation liegt dann also gar nicht vor. Ansonsten wird das Zellenfeld in fünf Stücke aufgeteilt; ganz links, ganz rechts sowie in der Mitte wird der Minimalwert verwendet, dazwischen der im Parameterfenster eingestellte Maximalwert. Die Übergänge zwischen den Bereichen werden durch Polynome dritten Grades geschaffen. Wie die Verteilung der Größe des des Parameters b_b(x) bei Einstellung des Wertes 0.02 aussieht, zeigt die Abbildung 1. Im Übergang der Bereiche schneller und langsamer Oszillation kann es - je nach Phasenverschiebung - zu Anregungen (neue Linien) oder auch umgekehrt zu Deaktivierungen (Linienabbruch) kommen.
Einen weiteren Zweikampf lohnt es anzuschauen: Man stelle den Maximalwert für die Grundproduktion an Substrat auf 0.02 ein und die beiden Diffusionskonstanten auf 0.01. Aus dem schönen Bild entstehen durch Anhebung der Diffusionskonstante des Subtrates skurrile Muster, die aus dem Ringen des Wellenmusters mit der ortsabhängig ausgeprägten Tendenz zum Übergang zum zeitlich stabilen Streifenmuster resultieren.

zur Einstiegsseite
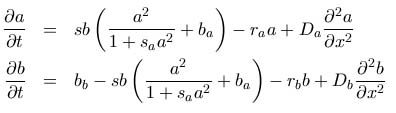