Muster mit senkrechten und waagerechten Streifen

Übergestreifte Muster

Streifen sind auf Schneckenschalen keine Seltenheit. Sie können senkrecht zur Wachstumskante verlaufen (ein zeitlich stabiles Muster) oder waagerecht zu ihr (Oszillation), aber durchaus auch schräg. Ebenso variabel wie die Ausrichtung ist die Breite der Streifen.

Im Gegensatz zur Kinetik chemischer Reaktionen gibt es in der Enzymkinetik das Phänomen der Sättigung: bei sehr hohen Substratkonzentrationen kann die Umsatzgeschwindigkeit nicht weiter gesteigert werden, d.h. es wird eine Maximalgeschwindigkeitswert erreicht. Chemische Umwandlungen in Zellen laufen - insbesondere bei höhermolekularen Stoffen - typischerweise enzymkontrolliert ab. Deshalb muss in ein gutes Modell das Sättigungsphänomen einfließen.
Den Grundstein für die Enzymkinetik legten Michaelis und Menten mit ihrer 1913 vorgestellten und nach ihnen benannten Michaelis-Menten-Gleichung. Aus ihr entwickelte man die sogenannte Inhibitionsgleichung, die hier in das Einfache Aktivator-Inhibitor-Modell eingearbeitet wird.

Die mathematische Formulierung

Das System partieller Differentialgleichungen für das Aktivator-Inhibitor-Modell mit Michaelis-Menten-Kinetik lautet wie folgt:

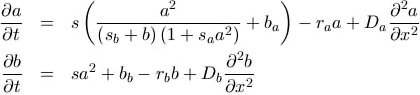
Ein Vergleich mit den Differentialgleichungen des Einfachen Aktivator-Inhibitor-Modells lässt sofort erkennen, dass beide Modelle für s_a = 0 und s_b = 0 übereinstimmen.

Mustersimulation und Wirkung der inhibitorischen Sättigung

Eine Simulation mit den voreingestellten Werten lässt diesmal ein anderes Bild erscheinen, obwohl beide Sättigungskoeffizienten tatsächlich verschwinden. Betrachtet man diese Werte, ist jedoch (Eingeweihten) sofort klar, dass ein Streifenmuster senkrecht zur Wachstumskante so nicht entstehen kann:

	Grundproduktion	Zerfallsrate	Diffusionskonstante	Sättigungskoeffizient
Aktivator	0.02	0.05	0.04	0
Inhibitor	0	0.03	0	0

Eine Voraussetzungen für senkrechte Streifen beim Einfachen Aktivator-Inhibitor-Modell war eine sehr viel größere Diffusionskonstante beim Inhibitor als beim Aktivator (mindestens Faktor 7). Die Parameter sind diesmal so eingestellt, dass die Aktivatormenge oszilliert: Es entstehen Streifen waagerecht zur Wachstumskante. Unter diesen Bedingungen kann man sich die Wirkung der beiden Sättigungskoeffizienten einmal anschauen.

• Erhöht man nur den Sättigungskoeffizienten des Aktivators, so erhöht sich die Oszillationsfrequenz (dichtere Linien), wohingegen die Amplituden sinken (Bild verschwimmt, wenn man das Muster in der relativen oder absoluten Variante betrachtet).
  [Erklärung: Der Zuwachs an Aktivator ist beschränkt, so dass keine großen Mengen erreicht werden (kleinere Amplitude), da auch die Inhibitormenge ansteigt. Diese bleibt jedoch ebenso geringer, da der Zuwachs an die (jetzt kleinere) Aktivatormenge gekoppelt ist. So kann sich der Aktivator schneller erholen (höhere Frequenz).]
• Erhöht man hingegen nur den Sättigungskoeffizienten des Inhibitors, so verringert sich die Oszillationsfrequenz bis hin zum völligen Verschwinden des Musters.
  [Für die Erklärung muss man schauen, wie der Parameter in der ersten Differentialgleichung wirkt.]
• Versucht man, beide Paramter gegeneinander antreten zu lassen, so stellt man fest, dass sich das auf die örtliche Konstanz der Oszillation auswirkt: die Linien tendieren zu einem Wellenverlauf. Außerdem bleibt es dabei, dass ein hoher Sättigungskoeffizient des Inhibitors auch dann zum Verschwinden des Musters führt.

Stellt man die drei gemeinsamen Parameter auf die Werte des Einfachen Aktivator-Inhibitor-Modells um, so sieht man die bekannten Streifen senkrecht zur Wachstumskante. Auch hier wirken sich Änderungen an den Sättigungskoeffizienten auf Streifenbreite und -dichte aus. Es gibt viele Möglichkeiten zum Probieren und Argumentieren, da diesmal kombinierte Änderungen nicht so häufig zu völligem Verschwinden des Musters führen.

zur Einstiegsseite