Zum mathematischen Modell von Meinhardt und Gierer

Die Idee antagonistischer Effekte bedingt die Mitwirkung von mindestens zwei verschiedenen Stoffen. Die mathematische Formulierung des Modells beruht auf einem System partieller Differentialgleichungen in der Zeitvariable t (Wachstumsrichtung) und der Ortsvariable x (Wachstumskante). Jeder an den Wechselwirkungen beteiligte Stoff bedingt eine Gleichung im System. Alle Gleichungen sind vom Prinzip her identisch aufgebaut:

Dabei ist a eine vektorwertige Funktion der Dimension n (= Zahl der beteiligten Stoffe) in den Variablen x und t. Die Wechselwirkungen zwischen den Koordinatenfunktionen werden durch die Funktion repräsentiert. Der Anteil beschreibt die Diffusion der zur Koordinatenfunktion a_i gehörenden Substanz, wobei der Faktor (die Diffusionskonstante) stets positiv ist und seine Größe direkt mit der Diffusionsgeschwindigkeit des Stoffes korreliert.

Für ein grundlegendes Muster soll der Modellansatz an dieser Stelle beispielhaft erörtert werden: Aus der Erläuterung des Zustandekommens der Schalenmuster begründet sich, dass Streifen senkrecht zur Wachstumskante als zeitlich stabile örtliche Muster angesehen werden müssen. Solche lassen sich mit dem Aktivator-Inhibitor-Prinzip erklären. An diesem konkreten Modell sind zwei Substanzen beteiligt. Die Ausbildung eines visuell erfassbaren Musters verlangt, dass mindestens einer der beteiligten Stoffe direkt (oder indirekt) für die Produktion eines Farbpigmentes verantwortlich zeichnet. Es wird angenommen dass ein Stoff a, der sogenannte Aktivtor, die Pigmentproduktion steuert. Er wirkt nur über kurze Entfernungen. [Man spricht in diesem Zusammenhang von der Reichweite eines Stoffes und meint damit die mittlere Entfernung zwischen dem Ort seiner Produktion und seines Zerfalls.] Außerdem fördert er seine eigene Produktion (Autokatalyse). Sein Antagonist (= Gegenspieler) ist die Substanz b, der Inhibitor, der sich schnell ausbreitet und über große Entfernungen wirkt. Der Aktivator fördert ebenso wie seine eigene auch die Produktion des Inhibitors, welcher aber seinerseits die Produktion des Aktivators a hemmt. In der Ausgangssituation befinden sich beide Stoffe in einem Gleichgewicht. Dieses erweist sich jedoch als instabil.
Wird versucht, die Balance durch eine globale Erhöhung der Aktivatorkonzentration zu stören, wird diese durch den dadurch bedingten Anstieg der Inhibitorkonzentration zurückgeregelt. Was jedoch, wenn die Zunahme der Aktivatorkonzentration nur lokal geschieht? (Örtlich gering schwankende Stoffmengen sind unter natürlichen Bedingungen sogar zu erwarten.) Aufgrund der Autokatalyse wird die Aktivatorproduktion lokal noch weiter gesteigert. Der damit einhergehende Anstieg auch der Inhibitorkonzentration kann diesmal aber nicht zu einer Rückführung in einen Gleichgewichtszustand führen, da der Inhibitor sich schnell in die Umgebung ausbreitet. Der sich rasch verbreitende Inhibitor bremst dafür die Autokatalyse des Aktivators in der Umgebung des Ausgangspunktes der Störung. Die Folge: am Ort des Auftretens der Störung wird die Aktivatorkonzentration hoch bleiben, in der unmittelbaren Umgebung jedoch niedrig. Das Gedankenexperiment erhofft sich das Entstehen eines zeitlich stabilen Streifenmusters (senkrecht zur Wachstumskante).
Dass sich auf Grundlage der Idee tatsächlich ein zeitlich stabiles Muster ergibt, ist im Vorhinein nicht klar. Nichtlineare Systeme mit Rückkopplungen besitzen üblicherweise Eigenschaften, die der menschlichen Intuition entgegenlaufen. Setzt man das soeben verbal Formulierte in Gleichungen um, so zeigen deren Lösungen jedoch tatsächlich das erhoffte Resultat, wenn gewisse Bedingungen an die Modellparameter erfüllt sind. Erste Voraussetzung ist, dass sich der Inhibitor sehr viel schneller ausbreitet als der Aktivator. Für das Entstehen des Musters muss daher der Wert der Diffusionskonstante des Inhibitors b die Größe desselben von a weit überschreiten. [Granero et al. zeigten 1977, dass hierfür mindestens der Faktor 7 nötig ist.] Hat sich das Aktivator-Inbhibitor-Verhältnis auf höherem Niveau (am Ort der Störung) wieder stabilisiert, dürfen neuerliche lokale Störungen auf das neue lokale Gleichgewicht keinen destabilisierenden Einfluss haben. Das ist nur dann gewährleistet, wenn der Inhibitor sehr schnell auf eine Veränderung der Aktivatorkonzentration reagieren kann. Dazu muss als eine zweite Voraussetzung der Inhibitor eine kürzere Lebensdauer haben als der Aktivator. Die Stabilität des Musters verlangt demnach für den Inhibitor eine höhere Zerfallsrate als für den Aktivator.
Die spezifischen Gleichungen für das Aktivator-Inhibitor-Prinzip lauten wie folgt:

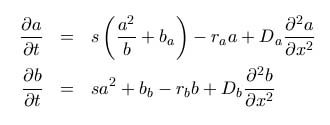
Die verbal formulierten Modellpostulate lassen sich leicht aus den Gleichungen ablesen: Der Term
beschreibt die Produktion an Aktivator zum Zeitpunkt t. Er hängt nichtlinear von der Konzentration von a selbst ab. Die katalytische Wirkung des Aktivators könnte beispielsweise aus einer Komplexbildung zweier einzelner Aktivatormoleküle resultieren, was zu einer quadratischen Abhängigkeit führt. Der Nenner sorgt für den hemmenden Einfluss des Inhibitors. Eine unabhängige Grundproduktion des Stoffes a wird durch b_a angezeigt, der gemeinsame Faktor s steht für die Quelldichte. [Die Grundproduktion ist vom übrigen System unabhängig. Unter Quelldichte versteht man die lokale(!) Produktionsrate, also eine von einer Stoffkonzentration abhängige Produktion. Ihre minimale Schwankung löst die lokalen Störungen aus.]
Die Lebensdauer der Substanz a wird durch die Zerfallsrate r_a bestimmt; das natürliche Verschwinden von Aktivatormolekülen zum Zeitpunkt t wird folglich durch den Term -r_aa beschrieben. Die annähernde Gleichheit der Werte der Quelldichte s, also der lokalen Produktionsrate, und der Zerfallsrate soll helfen, dass in den Simulationen Absolutkonzentrationen in der Größenordnung 1 entstehen.
In Bezug auf den Inhibitor verhält sich die Sache ähnlich. Auch für ihn ist eine unabhängige Grundproduktion denkbar (b_b), ansonsten wird sein Entstehen positiv von der Konzentration des Aktivators a beeinflusst (sa²). Sein Zerfall wird durch den Term -r_bb ausgedrückt.
Beiden Gleichungen gemein ist der die Diffusion beschreibende Term .
Die oben genannten Voraussetzungen, die für das Entstehen eines zeitlich stabilen Streifenmusters gemacht wurden, lauten jetzt ganz einfach D_b >> D_a sowie r_b > r_a.

Meinhardt stellt in seinem Buch weitere Modelle vor, die zu einfachen Mustern führen. Er betrachtet zusätzliche Phänomene (z.B. Sättigungseigenschaften) und ihre Wirkungsmöglichkeiten, wodurch er ein Grundverständnis für folgende Simulationen komplizierterer Muster schafft. Diese lassen sich durch zeitabhängige oder noch besser ortsabhängige Parameter wie auch durch das Einbringen weiterer Substanzen kreieren. Ebenso ist es möglich, Modelle zu verbinden: Dazu werden Modelle einfacher Muster parallel nebeneinander gestellt und dann durch zusätzlich eingefügte Terme miteinander verquickt.

Wer noch etwas zur Lösung des mathematischen Problems wissen möchte, folge diesem Link.

zur Einstiegsseite