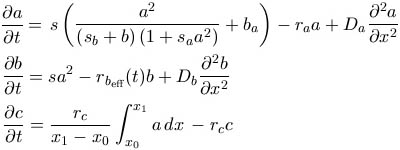Verzweigungen bei Oliva porphyria
Seltenes Ereignis
Streifenmuster, Punktmuster, Wellenlinien: Solche Muster findet man auf einigen Schalen der vielen
bekannten Arten tropischer Schnecken. Manche Muster sind jedoch außergewöhnlich. Zu ihnen zählen
sicher die Verzweigungen, die uns die Schalen von Oliva porphyria präsentieren.
Modellierung
-
Das Modell baut auf dem Aktivator-Inhibitor-Mechanismus mit Michaelis-Menten-Kinetik auf. Die Zerfallsrate
ist jedoch zeitlich nicht konstant: Sie wird durch einen dritten beteiligten, hormonähnlichen Stoff beeinflusst.
Meinhardt betrachtet in Wie Schnecken sich in Schale werfen das folgende Modell auf der Basis von
Zellen:
-
"In Abhängigkeit von der vorhandenen Aktivatorkonzentration
produzieren die Zellen ein Hormon, das sich so schnell ausbreitet,
dass seine Verteilung in allen Zellen homogen ist. (Aus dieser Annahme
resultiert eine Unabhängigkeit der zugehörigen Differentialgleichung vom Ort.) Die Hormonkonzentration wirke
auf die Zerfallsrate des Inhibitors, so dass diese zeitlich nicht
konstant ist. Zum Zeitpunkt t ergibt sie sich durch
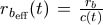 , wobei
c(t) die (nur von der Zeit abhängige) Hormonmenge ist. Diese wächst mit einer hohen Aktivatorkonzentration."
, wobei
c(t) die (nur von der Zeit abhängige) Hormonmenge ist. Diese wächst mit einer hohen Aktivatorkonzentration."
Mathematische Formulierung und Mustersimulation
Das verwendete System partieller Differentialgleichungen zur Simulation des Verzweigungsmusters von
Oliva porphyria lautet wie folgt:
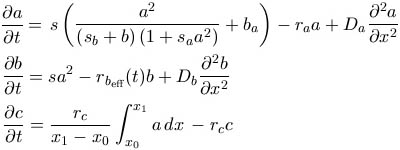
Dabei sind x0 und x1 die x-Koordinaten
des linken bzw. rechten Randes des Zellenfeldes.
Die Ortsunabhängigkeit der Differentialgleichung für das Hormon erlaubt es, sie bei Anwendung der Linienmethode
außer Acht zu lassen und den neuen Wert c(t) nach Abschluss eine kompletten Rechenschrittes vorzunehmen.
Damit man den Wert der Zerfallsrate des Hormones aber einfach im Parameterfenster einstellen kann, muss die
Gleichung angemeldet sein, weshalb eine Pseudogleichung für c definiert wurde. Das ist wichtig zu wissen,
wenn man sich hier einen Film von der Wachstumskante anschaut. Die unbewegliche weiße Linie, die angeblich die
Hormonkonzentration anzeigen soll, kann man getrost abschalten - sie sagt nichts aus. Da die Hormonmenge
ortsunabhängig ist, weiß man immerhin, dass die zugehörige Kurve eine parallele Linie zur Wachstumskante
bildet. Diese sollte sich dann nahezu periodisch auf- und abbewegen.
|
Grundproduktion |
Zerfallsrate |
Diffusionskonstante |
Sättigungskoeffizient |
| Aktivator |
0 |
0.1 |
0.015 |
0.25 |
| Substrat |
|
0.014 |
0 |
0.1 |
| Hormon |
|
0.1 |
|
|
zur Einstiegsseite