7. Numerische Beispiele
Um die mathematischen Methoden zur Rekonstruktion eines zweidimensionalen Bildes aus Projektionsdaten zu testen, simulieren wir die Datensammlung eines Computertomographen mit der in Abschnitt 4 beschriebenen Geometrie. Dazu geben wir uns ein Phantom vor, simulieren eine Messung mit einem Objekt, das im Querschnitt gerade die Materieverteilung unseres Phantoms hat und versuchen anschließend, das vorgegebene Phantom zu rekonstruieren. Wir haben so die Möglichkeit, die Qualität der Rekonstruktion mit dem exakten Bild zu vergleichen.
Für die folgenden numerischen Berechnungen verwenden wir die Parameter eines
Computertomographen mit Pmin = -258.97 mm, Pmax = 258.20 mm,
 min = 69°,
min = 69°,
 max = 248.38° und
einem quadratischen Bildgebiet
max = 248.38° und
einem quadratischen Bildgebiet 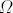 2 (vgl. Abb. 5) der Kantenlänge 300 mm.
2 (vgl. Abb. 5) der Kantenlänge 300 mm.
Unser Phantom entsteht durch Superposition von Elementarobjekten, die an gewünschten Positionen in beliebiger Orientierung und Größe sowie mit beliebigem Wert für die Dichte (evtl. negativ) platziert werden können. Die Dichte des Bildes in einem festen Punkt wird deffniert als die Summe der Dichten aller Elementarobjekte, in denen der Punkt liegt. Diese muss natürlich stets nichtnegativ sein. Als Elementarobjekte wollen wir uns an dieser Stelle der Einfachheit halber auf Ellipsen beschränken.
Zum Erstellen der rechten Seite b aus (7) verwenden wir für unsere Tests das Phantom aus
Abb. 7, das mit den Parametern aus Tabelle 3 erzeugt wurde. Dabei ist (Cx;Cy) der Mittelpunkt,
hx, hy sind die Halbachsen und  ist der Drehwinkel der Ellipse.
ist der Drehwinkel der Ellipse.

Abbildung 7. Standard Kopf-Phantom
| Nr. | Typ | Cx | Cy | hx | hy |  |
 |
|||||||||
| 1 | Ellipse | 0 | 0 | 120 | 140 | 0 | 2 | |||||||||
| 2 | Ellipse | 0 | -5 | 110 | 130 | 0 | -1.5 | |||||||||
| 3 | Ellipse | 0 | 60 | 30 | 40 | 0 | 1 | |||||||||
| 4 | Ellipse | 30 | 0 | 30 | 70 | -5 | -0.5 | |||||||||
| 5 | Ellipse | -30 | 10 | 15 | 50 | 5 | -0.5 | |||||||||
| 6 | Ellipse | 20 | -100 | 5 | 10 | 0 | 1 | |||||||||
| 7 | Ellipse | -20 | -100 | 10 | 5 | 0 | 1 | |||||||||
| Tabelle 3. Beschreibung der Elementarobjekte, die in Bild 7 verwendet wurden (in mm, Grad bzw. dm-1) |
||||||||||||||||
 |
Abbildung 8. Diskretisiertes Phantom, d.h. bestmögliche Lösung bei gegebener Auflösung (n = 16, n = 32, n = 64) |
Für die k-te Iterierte  (k)
= (
(k)
= ( 1(k)
,...,
1(k)
,..., n2(k))T
des cgls-Verfahrens aus Algorithmus 1 ist der Fehler der Rekonstruktion
n2(k))T
des cgls-Verfahrens aus Algorithmus 1 ist der Fehler der Rekonstruktion
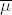 |
(k)(x) = | n2 |  i(k) i(k)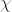 i i |
(x) |
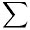 |
||||
| i = 1 |
durch e(k) := ||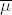 (k) -
(k) -  ||
||
gegeben, wobei  die exakte
Funktion für Schwächungskoefizienten (vgl. Abb. 7) und ||·|| die
L2-Norm ist. Sei
die exakte
Funktion für Schwächungskoefizienten (vgl. Abb. 7) und ||·|| die
L2-Norm ist. Sei  diskret eine Diskretisierung von
diskret eine Diskretisierung von  mit n×n Pixeln
(vgl. Abb. 8). Diese kann zum Beispiel durch Mittelung des Schwächungskoefizienten an einer
gewissen Anzahl gleichverteilter Punkte in einem Pixel deffniert werden. Ist
mit n×n Pixeln
(vgl. Abb. 8). Diese kann zum Beispiel durch Mittelung des Schwächungskoefizienten an einer
gewissen Anzahl gleichverteilter Punkte in einem Pixel deffniert werden. Ist  Lösung von (8) und
Lösung von (8) und 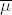 (x) =
(x) = 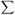 i=1n2
i=1n2
 i
i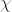 i(x), dann gilt
i(x), dann gilt
e(k) := ||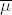 (k) -
(k) -  ||
||  ||
||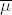 (k) -
(k) - 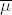 || + ||
|| + ||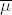 -
-  diskret || +
||
diskret || +
|| diskret -
diskret -  ||.
||.
Der Fehler der Rekonstruktion setzt sich also aus dem Fehler der Lösung des Gleichungssystems,
dem Modellierungsfehler und dem Diskretisierungsfehler zusammen. Dabei ist der Diskretisierungsfehler
um so kleiner, je größer die Anzahl der Pixel n2 und der
Modellierungsfehler um so kleiner, je größer die Anzahl der Strahlen, also je
größer n![]() und nP sind. Das Verhalten des Fehlers der Rekonstruktion ist in Abb. 9
dargestellt.
und nP sind. Das Verhalten des Fehlers der Rekonstruktion ist in Abb. 9
dargestellt.
Die Daten (4) zweier Durchleuchtungen des Phantoms sind in Abb. 10 als Funktion von  2 -->
2 -->  dargestellt. Hierbei sind auf
der x-Achse die n
dargestellt. Hierbei sind auf
der x-Achse die n![]() Winkelpositionen der um das Objekt rotierenden Apparatur und auf der y-Achse die
nP parallelen Strahlen je Winkelposition als Grauwerte aufgetragen. Abb. 11, 12
und 13 zeigen die Rekonstruktion des Schnittbilds nach 1, 8 und 30 Iterationen des cgls-Verfahrens
für verschiedene Auflösungen.
Winkelpositionen der um das Objekt rotierenden Apparatur und auf der y-Achse die
nP parallelen Strahlen je Winkelposition als Grauwerte aufgetragen. Abb. 11, 12
und 13 zeigen die Rekonstruktion des Schnittbilds nach 1, 8 und 30 Iterationen des cgls-Verfahrens
für verschiedene Auflösungen.
Auszüge aus dem Artikel "Mathematik fürs Leben am Beispiel der
Computertomographie"
Autoren: Marlis Hochbruck · Jörg-M. Sautter

