5. Diskretisierung
Neben der Diskretisierung der Umkehrformeln der Radontransformation (4) ergibt
sich eine andere Möglichkeit durch folgenden algebraischen Ansatz: Die Funktion
 aus (3) beschreibt auf dem
quadratischen Bildgebiet
aus (3) beschreibt auf dem
quadratischen Bildgebiet 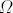 2,
welches das zu rekonstruierende Objekt enthält, die Dichteverteilung der Materie. Auf
2,
welches das zu rekonstruierende Objekt enthält, die Dichteverteilung der Materie. Auf
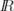 2\
2\ 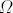 2 soll
2 soll  verschwinden. Mit Hilfe der Methode der finiten Elemente
wollen wir eine Näherungslösung
verschwinden. Mit Hilfe der Methode der finiten Elemente
wollen wir eine Näherungslösung 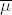 des Systems (4) berechnen. Dazu zerlegen wir wie in Abb. 5 skizziert das Quadrat
des Systems (4) berechnen. Dazu zerlegen wir wie in Abb. 5 skizziert das Quadrat
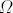 2 in n2
gleich große quadratische Elemente, im Folgenden Pixel genannt. Wir suchen eine Bestapproximation an die
Lösung von (4) im n2-dimensionalen Raum
2 in n2
gleich große quadratische Elemente, im Folgenden Pixel genannt. Wir suchen eine Bestapproximation an die
Lösung von (4) im n2-dimensionalen Raum
S = [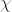 1
,...,
1
,...,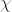 n2]
n2]
mit den Basisfunktionen 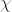 i :
i :
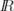 2 -->
2 -->
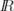 , i = 1,...,n2, die durch
, i = 1,...,n2, die durch
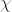 (k-1)n+ (k-1)n+ |
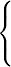 |
1, | falls x im Pixel in der k-ten Zeile und | (5) |
 -ten Spalte der Zerlegung liegt; -ten Spalte der Zerlegung liegt; |
||||
| 0, | sonst. |
(k, 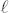 = 1,...,n) definiert sind. Die Funktionen
= 1,...,n) definiert sind. Die Funktionen
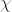 i, i = 1,...,n2,
sind also gerade die Indikatorfunktionen für die n2 Pixel. Wir stellen die gesuchte
Näherungslösung
i, i = 1,...,n2,
sind also gerade die Indikatorfunktionen für die n2 Pixel. Wir stellen die gesuchte
Näherungslösung 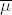 als
Linearkombination der Basisfunktionen
als
Linearkombination der Basisfunktionen 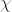 1
,...,
1
,...,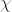 n2 dar:
n2 dar:
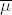 |
(x) = | n2 |  i
i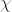 i i |
(x) |
 |
||||
| i = 1 |
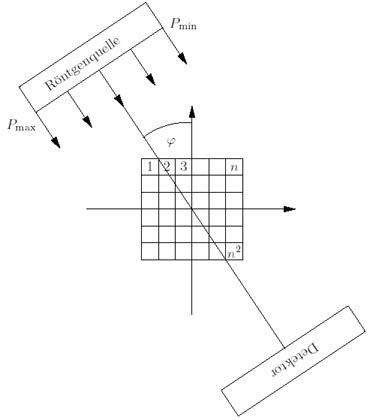
Abbildung 5. Approximation des Objekts durch endlichdimensionalen Teilraum.
 in
jedem Pixel der Zerlegung konstant und
in
jedem Pixel der Zerlegung konstant und  |
|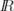 2\
2\ 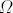 2
2  0. Das Bild, welches der Mediziner
später für seine Diagonse verwendet, entsteht durch Darstellung des Wertes im i-ten Pixel
(also von
0. Das Bild, welches der Mediziner
später für seine Diagonse verwendet, entsteht durch Darstellung des Wertes im i-ten Pixel
(also von  i) als Grauwert.
Die Diskretisierung ist also dem Problem angepasst. In der Praxis sind zur Zeit
Auflösungen von 512×512 Pixel gängig.
i) als Grauwert.
Die Diskretisierung ist also dem Problem angepasst. In der Praxis sind zur Zeit
Auflösungen von 512×512 Pixel gängig.Eingesetzt in (4) ergibt sich für i = 1,...,m
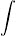 |
Li | 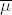 |
(x)dx = | n2 |  j
j |
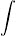 |
Li | 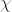 j
j |
(x)dx = bi. (6) |
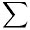 |
|||||||||
| j = 1 |
Mit A = ((aij )), A 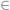
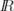 m,n2, wobei
m,n2, wobei
| aij | = | 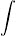 |
Li | 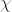 j
j |
(x)dx i = 1,...,m, j = 1,...,n2, |
 |
= | ( 1,..., 1,...,
 n2)T n2)T 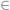  n2, n2, |
|||
| b | = | (b1,...,bm)T   m, m, |
|||
kann man (6) als lineares Gleichungssystem
Au = b (7)
mit dem unbekannten Koeffizientenvektor  und den gemessenen Werten der rechten Seite b schreiben. Die Formel für aij
besagt, dass das (i, j)-te Element von A gerade die Länge des Schnitts des i-ten
Strahls mit dem j-ten Pixel ist.
und den gemessenen Werten der rechten Seite b schreiben. Die Formel für aij
besagt, dass das (i, j)-te Element von A gerade die Länge des Schnitts des i-ten
Strahls mit dem j-ten Pixel ist.
Die Zahl der Messungen (d. h. die Zahl der Gleichungen im linearen Gleichungssystem (7)) wird gewöhnlich
wesentlich größer sein als die Anzahl der Pixel, um die Qualität der Rekonstruktion zu
erhöhen. Somit ergibt sich ein überbestimmtes lineares Gleichungssystem sehr großer
Dimension m×n2, dessen Koeffizientenmatrix A aber schwach besetzt ist, d.h. nur wenige
Einträge von A sind von Null verschieden, vgl. Abb. 6 und Tab. 2.
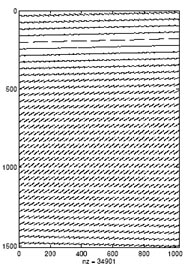 |
Abbildung 6. Struktur der Matrix A für n = 32, n |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabelle 2. Werte für die Rekonstruktion aus Abschnitt 7. In der Spalte nnz(A) ist der Anteil der von Null verschiedenen Elemente in A, in der letzten Spalte der Speicheraufwand in Megabyte angegeben. |
Es gilt die folgende Abschätzung:
Satz 1 In einer Zeile der Matrix A sind höchstens 2n-1 Elemente von Null verschieden.
Diese Aussage folgt durch einfache geometrische Überlegungen, die am Besten an Hand von Skizzen
nachzuvollziehen sind. Wir geben dennoch auch einen formalen Beweis.
Beweis. Die Elemente der i-ten Zeile von A sind die Längen des Schnitts der Geraden
Li mit den Pixeln der Zerlegung von  2. Ist Li parallel zu einer der beiden
Achsen, so schneidet Li genau n Pixel, da wir eine Kante immer nur einem Pixel
zuordnen. Es bleibt also nur der Fall Li streng monoton zu untersuchen.
2. Ist Li parallel zu einer der beiden
Achsen, so schneidet Li genau n Pixel, da wir eine Kante immer nur einem Pixel
zuordnen. Es bleibt also nur der Fall Li streng monoton zu untersuchen.
Ohne Einschränkung sei Li streng monoton fallend (den Fall
Li streng monoton wachsend behandelt man analog). Hat Li eine Steigung
größer als -1, so steht die Annahme Li schneide drei oder mehr
Pixel der j-ten Spalte der Zerlegung (1  j
j  n) sofort im Widerspruch dazu,
dass die Pixel quadratisch sind. Da j beliebig war, schneidet Li in jeder
Spalte der Zerlegung höchstens zwei Pixel. Es bleibt noch zu zeigen, dass es nicht möglich
ist, dass in jeder Spalte zwei Pixel geschnitten werden. Dies beweisen wir durch Widerspruch:
Angenommen, dies wäre der Fall. Nehmen wir also an, in der k-ten Spalte, 1
n) sofort im Widerspruch dazu,
dass die Pixel quadratisch sind. Da j beliebig war, schneidet Li in jeder
Spalte der Zerlegung höchstens zwei Pixel. Es bleibt noch zu zeigen, dass es nicht möglich
ist, dass in jeder Spalte zwei Pixel geschnitten werden. Dies beweisen wir durch Widerspruch:
Angenommen, dies wäre der Fall. Nehmen wir also an, in der k-ten Spalte, 1
 k
k  n, wären dies Pixel
n, wären dies Pixel  und
und  +1, 1
+1, 1 
 < n, dann müssen es in der
(k+1)-ten Spalte Pixel
< n, dann müssen es in der
(k+1)-ten Spalte Pixel 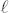 +1 und
+1 und 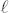 +2
sein, usw. Offensichtlich bekommen wir die maximale Anzahl von Pixeln mit nicht leerem Schnitt mit
Li für k = 1 und
+2
sein, usw. Offensichtlich bekommen wir die maximale Anzahl von Pixeln mit nicht leerem Schnitt mit
Li für k = 1 und 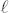 = 1. In der n-ten Spalte würden dann die Pixel n und
(n+1) geschnitten, im Widerspruch dazu, dass die n-te Spalte nur n Pixel hat. Es
ist also nicht möglich, dass in der ersten und der letzten Spalte zwei Pixel von
Li geschnitten werden.
= 1. In der n-ten Spalte würden dann die Pixel n und
(n+1) geschnitten, im Widerspruch dazu, dass die n-te Spalte nur n Pixel hat. Es
ist also nicht möglich, dass in der ersten und der letzten Spalte zwei Pixel von
Li geschnitten werden.
Analog schneidet ein Strahl mit einer Steigung kleiner oder gleich -1 in
jeder Zeile der Zerlegung höchstens zwei Pixel; jedoch niemals zwei Pixel in der ersten
und in der letzten Zeile.
Insgesamt haben also höchstens 2n-1 Pixel einen nichtleeren Schnitt
mit Li. 
Das lineare Gleichungssystem (7) ist daher überbestimmt und i.A. nicht lösbar
oder nicht eindeutig lösbar. Wir suchen deshalb eine Lösung 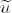 im Sinne der kleinsten Quadrate
(Carl F. Gauß, 1809), d.h.
im Sinne der kleinsten Quadrate
(Carl F. Gauß, 1809), d.h.
Q(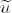 ) := ||b - A
) := ||b - A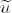 ||2
||2  Q(
Q( ) für alle
) für alle 
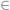
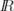 n2
(8)
n2
(8)
Bekanntlich ist 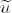 Lösung der Normalengleichungen
Lösung der Normalengleichungen
ATAu= ATb.
Die Lösung ist genau dann eindeutig bestimmt, wenn A vollen Spaltenrang hat.
Auszüge aus dem Artikel "Mathematik fürs Leben am Beispiel der
Computertomographie"
Autoren: Marlis Hochbruck · Jörg-M. Sautter

