4. Mathematisches Modell

Ziel ist es, die ortsabhängigen Schwächungskoeffizienten eines Querschnitts des zu untersuchenden Objektes zu bestimmen. Deshalb reicht es aus, die Einschränkung von auf die Querschnittsebene zu betrachten. Der ortsabhängige Schwächungs- koeffizient des Querschnitts kann also durch eine zweidimensionale Absorptionsfunktion

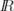: ² --> 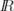,   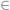L².    (3)

beschrieben werden. Die Funktion lässt sich nun durch den Intensitätsverlust der Röntgenstrahlung durch Absorption bei Durchleuchtung des Objekts aus vielen verschiedenen Richtungen bestimmen. Dazu rotieren Röntgenquellen und Detektoren in der Querschnittsebene um das Objekt und durchstrahlen es mit parallel ausgesandten Röntgenstrahlen (vgl. Abb. 4). Je nach Konstruktion des Computertomographen sind auch fächerförmig ausgesandte Röntgenstrahlen üblich. Im Folgenden gehen wir aber von einer parallelen Durchstrahlung aus, wobei die hier beschriebene Methode zur Bestimmung der Absorptionsfunktion (3) auch für fächerförmig ausgesandte Röntgenstrahlen mit leichten Modifikationen gültig ist.

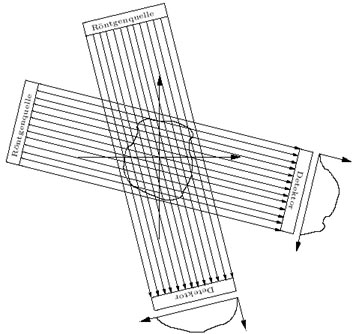
Abbildung 4. Prinzipieller Aufbau eines Computertomographen.

Die Apparatur rotiere in n gleichverteilten Schritten zwischen min und max und jedes Strahlenbündel bestehe aus n_P gleichverteilten Strahlen zwischen P_min und P_max (vgl. Abb. 5).

Die Messungen mit dieser Geometrie liefern m := n n_P Werte der Linienintegrale (2) über die linearen Abschwächungskoeffizienten entlang der Geradenstücke L_j; j = 1,...,m, von den Quellen zu den Detektoren. Bezeichnen wir mit Quelle_j und Detektor_j die durch das j-te Geradenstück L_j verbundenen Quellen und Detektoren, j = 1,...,m, und mit I_Quellej bzw. I_Detektorj die zugehörigen Intensitäten, so gilt nach (2)

IDetektorj = IQuellej

exp(-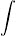

Lj

(x)dx).

Äquivalent dazu ist

ln	IDetektorj	= -		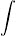Lj		(x)dx	.
	IQuellej

Zur Rekonstruktion der linearen Abschwächungskoeffizienten müssen wir das Integralgleichungssystem

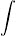Lj

(x)dx) = bj,  j = 1,...m.    (3)

lösen. Dabei sind die b_j die experimentell ermittelten Werte:

Durch Streuung der Strahlung im Objekt sind die experimentell ermittelten Werte in der Praxis allerdings noch mit einer Störung behaftet.

Gleichung (4) ist die Radontransformation (vgl. [12]) der Funktion . Bei (geeignet gewählten) unendlich vielen Strahlen ist eindeutig durch die rechten Seiten bestimmt; bei endlich vielen Strahlen lässt sich nur approximativ bestimmen. Umkehrformeln sind zwar bekannt (vgl. zum Beispiel [11]), jedoch für den mit diesem Projekt angesprochenen Schüler- und Studierendenkreis ohne weitere Vorbereitung schwierig zu handhaben. Im nächsten Abschnitt stellen wir daher eine numerische (approximative) Lösung von (4) für endlich viele Strahlen vor, die für die Praxis ausreichend genaue Näherungslösungen liefert.

WeiterZurück

Auszüge aus dem Artikel "Mathematik fürs Leben am Beispiel der Computertomographie"
Autoren: Marlis Hochbruck · Jörg-M. Sautter

Kompletter Artikel (pdf)