6. Numerische Lösung
Wegen der großen Dimension von A ist eine direkte Lösung von (8) - etwa mit Hilfe von Gauß-Elimination (bzw. Cholesky-Zerlegung) oder QR-Zerlegung (vgl. [6]) - des Minimierungsproblems nicht mehr effzient möglich. Die Ursache dafür liegt darin, dass die berechnete Zerlegung nicht mehr dünn besetzt ist. Der Rechenaufwand für die direkte Lösung liegt in der Größenordnung n6, wenn mit einer Auflösung von n×n Pixeln gerechnet wird. Bei n = 512 wird diese Berechnung selbst auf den immer schneller werdenen Computern auch in naher Zukunft nicht in vernünftiger Zeit möglich sein. Der Speicheraufwand ist mit 8n4 Bytes ebenfalls inakzeptabel hoch: Bei optimaler Programmierung würde die Lösung auf einem Rechner mit einer Taktfrequenz von 2 GHz und mindestens 550 GB Hauptspeicher mehr als einen Monat dauern.
Eine effziente Lösung muss daher iterative Verfahren wie das Verfahren des
steilsten Abstiegs, das Verfahren der konjugierten Gradienten (cg-Verfahren) oder
das Kaczmarz-Verfahren verwenden. Prinzipiell eignen sich alle Verfahren, bei denen
die Matrix A nur in Form von Matrix-Vektor Produkten eingeht, also wo nur A und ggf. AT
und ggf. AT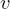 für Vektoren
für Vektoren  und
und 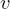 berechnet werden müssen.
Hierfür müssen nämlich nur die von Null verschiedenen Einträge von A
gespeichert werden, was sich mit dem in Tabelle 2 aufgeführten Speicherbedarf realisieren
lässt. Zum Vergleich: Für n = 512 sind für die Speicherung von A nur
1,7 GB, für ATA jedoch 550 GB erforderlich.
berechnet werden müssen.
Hierfür müssen nämlich nur die von Null verschiedenen Einträge von A
gespeichert werden, was sich mit dem in Tabelle 2 aufgeführten Speicherbedarf realisieren
lässt. Zum Vergleich: Für n = 512 sind für die Speicherung von A nur
1,7 GB, für ATA jedoch 550 GB erforderlich.
Die Idee des Verfahrens der konjugierten Gradienten zur Lösung eines linearen
Gleichungssystems
M = g, M
= g, M 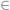
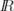 ñ,ñ, g
ñ,ñ, g 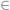
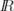 ñ
ñ
mit symmetrischer und positiv definiter Matrix M besteht darin, das Minimum der quadratischen
Funktion ||g - M ||2
nicht im gesamten hochdimensionalen Raum
||2
nicht im gesamten hochdimensionalen Raum 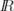 ñ sondern nur im niedrigdimensionalen affinen Teilraum
ñ sondern nur im niedrigdimensionalen affinen Teilraum
Kk(M,g) =  (0)
+ Span{g,Mg,M2g,...,Mk-1g},
(0)
+ Span{g,Mg,M2g,...,Mk-1g},
dem verschobenen k-ten Krylov-Raum bzgl. M und g, zu bestimmen. Man kann zeigen, dass dies möglich ist, indem man in jedem Teilschritt nur ein eindimensionales Minimierungsproblem löst. Details hierzu findet man in den meisten Numerik-Lehrbüchern, zum Beispiel in [6].
In unserem Fall ist M = ATA, g = ATb und ñ =
n2. Eine Variante des cg-Verfahren angewandt auf die Normalengleichungen ist das
cgls-Verfahren, siehe zum Beispiel [6]. Ein Pseudo-Code hierfür ist in Algorithmus 1 angegeben.
Die wichtigsten Eigenschaften des cgls-Verfahrens sind im folgenden Satz zusammengefasst.
Satz 2 [6] Die k-te Iterierte des cgls-Verfahrens liegt im verschobenen Krylov-Raum
 (k)
(k) |
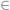 |
 (0) + Kk(ATA,ATr(0))
(0) + Kk(ATA,ATr(0)) |
| = |  (0) + Span{ATr(0),(ATA)ATr(0),
...,(ATA)k-1ATr(0)},
(0) + Span{ATr(0),(ATA)ATr(0),
...,(ATA)k-1ATr(0)}, |
wobei r(0) = b - A (0) das Anfangsresiduum ist. Unter allen Elementen
(0) das Anfangsresiduum ist. Unter allen Elementen  dieses affinen Raumes minimiert
dieses affinen Raumes minimiert
 (k) die Residuennorm ||b - A
(k) die Residuennorm ||b - A ||.
||.
Das cgls-Verfahren berechnet zwar theoretisch die exakte Lösung nach höchstens n2 Schritten, jedoch ist dieses Resultat für die Praxis aus verschiedenen Gründen irrelevant. Zum einen ist das Gleichungssystem selbst bereits durch diverse Näherungen konstruiert worden (vor allem durch die Diskretisierung in Pixel und die Annahme, dass in jedem dieser Pixel die Dichte konstant ist). Zum anderen wäre der Aufwand für n2 Schritte des Iterationsverfahrens mit dem eines direkten Verfahrens vergleichbar und daher inakzeptabel. Schließlich ist Satz 2 nur bei exakter Rechnung, d.h. ohne Berücksichtigung von Rundefehlern, richtig. Die Bedeutung des Verfahrens der konjugierten Gradienten liegt darin, dass es häufig schon nach wenigen Schritten brauchbare Näherungen berechnet, nämlich solche, deren Fehler in der Größenordnung des Diskretisierungsfehlers liegen. Wie wir später bei den numerischen Ergebnissen sehen werden, genügen für das CT-Problem tatsächlich weniger als 10 Schritte; die Lösung kann damit innerhalb von Sekunden berechnet werden (im Vergleich zu einem Monat bei direkter Lösung).
Algorithmus 1 Verfahren der konjugierten Gradienten zur
Lösung von ATA = ATb (cgls-Verfahren) = ATb (cgls-Verfahren) |
||
Wähle  (0) (0) 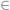 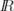 n2, setze
r(0) = b - A n2, setze
r(0) = b - A (0), s(0) = ATr(0) und wähle eine
Toleranz tol > 0;
(0), s(0) = ATr(0) und wähle eine
Toleranz tol > 0; |
||
Initialisiere k = 0, p(0) = s(0), 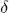 0 = (s(0))
Ts(0); 0 = (s(0))
Ts(0); |
||
while ||r(k)||  tol do tol do |
||
Berechne 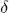 'k
= (Ap(k))T(Ap(k)); 'k
= (Ap(k))T(Ap(k)); |
||
Berechne  k = k = 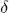 k/ k/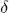 'k; 'k; |
||
Setze  (k+1) = (k+1) =
 (k) + (k) +  kp(k); kp(k); |
||
Berechne r(k+1) = r(k) -  kAp(k); kAp(k); |
||
| Berechne s(k+1) = ATr(k+1); | ||
Berechne 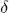 k+1
= (s(k+1))Ts(k+1), k+1
= (s(k+1))Ts(k+1),  k = k = 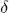 k+1/ k+1/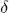 k; k; |
||
Setze p(k+1) = s(k+1) +  kp(k); kp(k); |
||
| Ersetze k durch k+1. | ||
| end while | ||
Der Genauigkeit der Rekonstruktion sind neben der Lösung des linearen Gleichungssystems und der Auflösung bei der Ortsdiskretisierung auch physikalische Grenzen gesetzt: Die maximale Auflösung von Feinstrukturen ist bereits durch die Dicke des Strahlenbündels limitiert. Innerhalb eines Elementquaders kann das Schwächungsvermögen der Materie nicht differenziert werden. Jeder errechnete lokale Schwächungskoeffzient stellt somit einen Mittelwert der Schwächung in seiner quaderförmigen Umgebung dar.
Auszüge aus dem Artikel "Mathematik fürs Leben am Beispiel der
Computertomographie"
Autoren: Marlis Hochbruck · Jörg-M. Sautter

